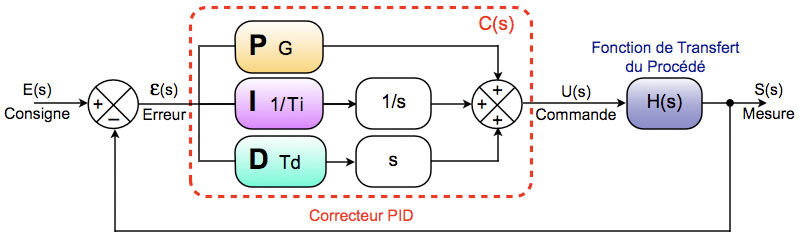
Asservissement

CECI EST UNE VULGARISATION

Un régulateur/asservissement PID c'est quoi?

Imaginons un régulateur de voiture dans une vitesse, ou l'inverse plutôt, mais je suis fatigué.

E = la consigne

S = la mesure

U = la commande,

ε = erreur = E - S

E c'est ce qu'on veut obtenir, admettons dans un premier temps qu'on veuille faire du 100km/h

S c'est ce qui est affiché au compteur

ε, si je ne roule qu'à 90, ça fait 100 - 90 = 10km/h

U, la pression que j'exerce sur l'accélérateur (ou le frein si on passe en négatif)

Correcteur proportionnel (P)

Je veux corriger tout ça, je fais quoi? Bin j'appuie sur l'accélérateur non! Et j'appuie d'autant plus fort que ma vitesse est basse. Et si je vais trop vite? Je lâche la pédale, et je la lâche d'autant plus que je veux ralentir.

En maths: U=(E-S)*P (ça s'appelle une loi de commande, et celle-ci c'est celle d'un correcteur proportionnel (P))

P c'est une constante de merde qui décrit à quel point on veut avoir ce comportement (et puis il en faut une de toute façon, juste pour les unités)

Correcteur proportionnel intégrateur (PI)

Jusqu'ici on a fait une commande proportionnelle à l'erreur. Cette décision n'est basée que sur un état à un instant donné. On ne tient pas compte des états précédents. Testons avec un paramètre bidon (ou presque). Ah merde, c'est pas assez, ça accélère jusque 95 mais on est pas encore à 100. Il y a ce qu'on appelle une erreur statique de 5km/h": une erreur qui finit par se stabiliser.

Bon, je vais essayer d'augmenter P... 96km/h, 97, 98... Encore un peu et c'est bon...

Ah merde! Ca fait n'importe quoi! Eh oui, si on met un P trop grand, on atteint un état instable: la voiture accélère.. mais c'est trop! Donc elle ralentit... mais trop! Donc elle raccélère... et c'est de pire en pire. Bref, FAIL. Avec un simple P, on aura toujours une erreur statique.

Comme dit précédemment, on a pas tenu compte des états précédents. C'est peut être pas top. Et si on regardait aussi le passé? Par exemple, si ça fait 5 min qu'on galère avec une erreur statique de 5km/h, il faudrait peut être plus accélérer que si c'est juste passager... On va donc prendre en compte le cumul dans le temps de cette erreur. -> Nouvelle loi de commande: le proportionnel intégrateur (PI):

U=(E-S)*P + cumul(E-S)*I

Cette fois ci, en choisissant les constantes comme il faut (on va y revenir), on peut être stable, et avoir une erreur statique nulle.

Correcteur proportionnel intégrateur dérivateur (PID)

Quoi? Pourquoi encore faire des maths alors que ça marche déjà? Parce que si on rajoute un terme, qui observe la tendance à décroitre ou à accroitre de l'erreur, on peut être plus réactif. En gros, si on définit une marge d'erreur acceptable, on l'atteint plus vite que dans le cas précédent. Ça marche un peu comme un trader qui regarde les courbes des cours de bourse. Si ça se casse la gueule sérieux, même si l'action vaut cher et qu'elle a monté depuis un bout de temps, là ça sent le roussi! Oui on doit pouvoir coder un trader avec un PID.

Ah oui, la formule pour les masos: U=(E-S)*P + cumul(E-S)*I + tauxDeCroissance(E-S)*D

Choix des constantes (les fameux P, I et D)

Il y a plusieurs méthodes, on peut tout modéliser et faire des calculs pour trouver les bonnes valeurs. Ca marche bien (souvent du premier coup), mais ça fait plein de calculs.

On peut aussi procéder par tâtonnement (il y a quand même une méthode), ça fonctionne très bien, surtout quand on ne sait pas comment modéliser, mais en contrepartie on passe un peu de temps à tourner des boutons.

En général, on vise le régime critique, c'est à dire les constantes qui rendent le bouzin le plus réactif possible sans pour autant le rendre instable.